主席树

Chivas-Regal

# 定义

可持久化线段树也叫函数式线段树、主席树
其对于每个修改并不是直接对一个节点更改它的值
而是对于这个节点额外创建一个节点表示它修改后的值，也被称为一个新的版本节点
对于这个版本节点，依然可以直接访问它的左右子节点、也可以直接访问它

# 可持久前提

本身的拓扑结构在整个操作中保持不变

树状数组，线段树，字典树，并查集，堆....都满足
但平衡树不可，平衡树有左旋右旋，节点之间的拓扑序会变

# 操作

# 查询

对于每次查询，我们需要确定版本
对于某个版本下的树，利用线段树的二分性质，二分地向下查询（和普通的差不多）

# 修改

每次单点修改会改变 $logn$ 个节点
因为向下递归，找到要修改的点后，一步步向上
从当前节点到根节点的一条路径上都要修改

区间修改很难实现，懒标记可以采用永久化懒标记进行维护

# 经典问题：区间第k小

# 前置知识：权值线段树

对值域内每个数出现的次树建立线段树

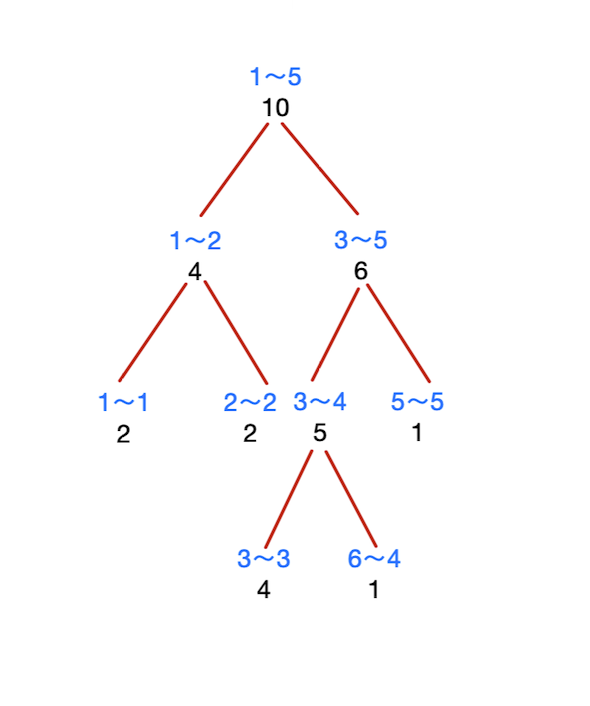
比如说 $1\;1\;2\;2\;3\;3\;3\;3\;4\;5$ 这个序列
会形成这样一棵权值线段树

想要求得此序列中的第k小，此时利用权值线段树的性质
我们可以二分地往下走
若左侧的个数 $\ge k$ ，走左侧 $(k)$
若左侧的个数 $\lt k$ ，走右侧 $(k-cnt_left)$
走到最后就是第 $k$ 小

# 快速求区间权值线段树

由于是区间查询
所以可以联想到前缀处理
即构建一棵前缀的权值线段树
那么我们在访问区间权值线段树时，可以两个前缀相减快速求得
相减操作包括访问操作，都可以用主席树去实现
对于序列中的每一个离散化之后的数，我们都可以将插入视作建立一个新版本
在查询区间的时候只需要查询两个版本即可

# 程序

逐个分析:

# 全局变量

const int N = 2e5 + 10;
int a[N];           // 原数组
vector<int> nums;   // 离散化数组
struct node {
    int l, r, sum;  // 左子树版本号，右子树版本号，当前版本数字个数
} sgtr[N * 30];     // 下标为版本号
int tot;            // 递进的版本号
int root[];         // 每个大版本 “[1~n]”  的出发节点

1
2
3
4
5
6
7
8

# 离散化

// 访问x离散化之后的值
inline int get_Id ( int x ) {
        return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}

1
2
3
4

# 插入

// 从数值 [l,r] 中查找 p 的位置从而修改，
// pre：当前节点的原先版本，不修改，用作实例
// now：我们要对这个原先版本新开的版本
inline void Insert ( int l, int r, int pre, int &now, int p ) {
        sgtr[++ tot] = sgtr[pre];       // 很多信息一样，剩下的改改就行
        now = tot;                      // 当前节点编号 = 新分配的节点编号
        sgtr[now].sum ++;               //这个节点数字的个数+1
        if ( l == r ) return ;          // 叶子节点

        int mid = (l + r) >> 1;
        // 插入什么数 -> 在线段树哪一个位置插入
        // 不仅我们要移动当前版本now至左(右)，我们也要移动我们的示例版本pre至左(右)
        if ( p <= mid )                 
                Insert(l, mid, sgtr[pre].l, sgtr[now].l, p);
        else
                Insert(mid + 1, r, sgtr[pre].r, sgtr[now].r, p);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 查询

// 版本号：R 和 L  
// 区间 [l,r] 固定出第 k 小在这之内
inline int Query ( int l, int r, int L, int R, int k ) {
        if ( l == r ) return l;

        int mid = (l + r) >> 1;
        // sgtr[sgtr[R].l].sum：版本 R 的左子树的 sum
        // sgtr[sgtr[L].l].sum：版本 L 的右子树的 sum
        // 新减出的线段树的左子树有多少个数
        int cnt = sgtr[sgtr[R].l].sum - sgtr[sgtr[L].l].sum; 
        // 版本 L R 都要向下移动至其 左(右)子树
        if ( k <= cnt )
                return Query(l, mid, sgtr[L].l, sgtr[R].l, k);
        else
                return Query(mid + 1, r, sgtr[L].r, sgtr[R].r, k - cnt);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 主函数

int main() {
        int n, m; cin >> n >> m;
        for ( int i = 1; i <= n; i ++ ) {
                cin >> a[i];
                nums.push_back(a[i]);
        }
        sort ( nums.begin(), nums.end() );
        nums.erase(unique(nums.begin(), nums.end()), nums.end());

        // 构建
        for ( int i = 1; i <= n; i ++ ) {
                Insert(1, n, root[i - 1], root[i], get_Id(a[i])); // 插入，同时赋值第i个数形成的版本号的出发根节点
        }

        while ( m -- ) {
                int l, r, k; cin >> l >> r >> k;
                cout << nums[Query(1, n, root[l - 1], root[r], k) - 1] << endl; // 前缀和思想，从 r 版本减去 l-1 版本进行查找
        }
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

FHQ-Treap Hash