线性DP

线性DP是几乎所有DP的基础，也是理解很多算法的基础

导引问题：超级楼梯

数据量大的话递归会超时。递推式？
每一个台阶带位置可以由它下面两层台阶转化而来，所以有递推式 $f(n)=f(n-2)+f(n-1)$

概述

概念

动态规划(Dynamic Programming，简称DP)是运筹学的一个分支，他是解决多阶段决策过程最优化的一种数学方法，把多阶段问题转变为一系列相互联系的单阶段问题(子问题)，然后逐个加以解决


简单的模型：一条有向无环图

$$...\stackrel{\color{green}转移}{\longrightarrow}\stackrel{\color{brown}决策}|{\color{blue}状态}\stackrel{\color{green}转移}{\longrightarrow}\stackrel{\color{brown}决策}|{\color{blue}状态}\stackrel{\color{green}转移}{\longrightarrow}\stackrel{\color{brown}决策}|{\color{blue}状态}\stackrel{\color{green}转移}{\longrightarrow}...$$

状态

状态是指一个阶段的信息表示，比如 $dp[x][y]$ 中的状态就是在此阶段， $dp$ 的就是对 $x$ 和 $y$ 的一种表示形式

决策

决策是一个阶段中，转移结束后对信息的选取，比如说决定走到 $dp[i]$ 时使用下面两个数的最大值就是一种决策

多阶段决策过程

在每一个阶段都要做出决策，从而使整个过程达到最优。各个决策选取仅依赖当前状态,从而确定输出状态，当各个阶段决策确定后，就组成了一个决策序列，这个决策序列就决定了问题的最终解决方案。这是一个前后关联具有链状结构的多阶段过程。

子问题

DP是按照一定次序分成相互联系的子阶段，一个大问题化成一族互相联系、同类型的子问题。

状态转移方程

对于同类子问题，设计一个固定的公式(即计算过程)保证在这条有向无环图中进行正确的移动

思想

是多种算法思想的组合算法

1. 穷举思想（在选择中决策）
2. 贪心思想（找最优决策）
3. 分治思想（拆分出子问题）
4. 递推、递归

过程

判断题目是否为DP
划分阶段
状态表示（设计程序）
状态转移方程
转移时的限制条件

经典题型

（最长上升子序列）LIS

思路1: 贪心、二分优化

我们贪心地去想
每一位能否加入我们的答案 其实取决于我们当前答案子序列里面的最后一位是不是比我们枚举到的这一位要小
所以我们要尽可能让最后一位变小
同时最后一位能否正确的变小 其实取决于我们前面的数是不是足够小
因为我们要保证我们的答案是一个上升的

在上升序列中我们枚举到位置 $i$ 时可以使用二分来看我们要替换哪一位让它尽可能变小 或者没有比它大的话就加入到我们的答案中
在此过程中顺序是会被打乱的
但是我们要知道的是：
我们是否改变答案长度，是根据我们是否加数来定的，而是否加数，是根据最后一位来定的，当我们加进去一个新数的时候，其实在那时也满足了一个LIS
时间复杂度： $O(nlogn)$

int a[1000005];
vector<int> vec;

int main(){
    int n; read(n);
    for(int i = 1, x; i <= n; i ++)  read(a[i]);
    for(int i = 1, x; i <= n; i ++){
        if(vec.empty() || vec.back() < a[i]) vec.push_back(a[i]);//这个是最大的就塞到队尾
        else                                 vec[lower_bound(vec.begin(), vec.end(), a[i]) - vec.begin()] = a[i];//能变小的话替换一下
        //其实顺序被打乱了，但是在求解size的时候并不影响，因为我们打乱完一遍也就是一个新的子序列，打乱一半是无影响的
    }write(vec.size());
    return 0;
}

思路2: 线性DP

可以用 $n^2$ 的复杂度去解
在上升子序列中，考虑每一位都必须比前面那一位要大
我们设置 $dp[i]$ 表示从第1位到第i位的最长上升子序列
所以我们在枚举每一位(设为 $a[i]$ )的时候
都利用前面的dp最优解去查一下
如果有一位(设为 $a[j]$ )的值小于 $a[i]$
那么我们完全可以把 $a[i]$ 放到 $a[j]$ 后面，得到的这一种子序列 $dp[i]=dp[j]+1$
时间复杂度： $O(n^2)$

const int N = 1005;

int a[N];
int dp[N];
int res;

int main(){
    int n; read(n);
    for(int i = 1, x; i <= n; i ++)  read(a[i]);
    for(int i = 1; i <= n; i ++){ dp[i] = 1;//初始化为1，因为自己本身一个数就是一个LIS
        for(int j = 1; j < i; j ++) if(a[j] < a[i]) dp[i] = MAX(dp[j] + 1, dp[i]);//如果前面的某一位小于当前的这一位，完全可以把这一位接到前面那一位后面
        res = MAX(res, dp[i]);//维护一下最大答案
    }write(res);
    return 0;
}

（最长公共子序列）LCS

思路：转化LIS

因为a中每个数只出现过一次，所以在这道题里面，我们可以将问题转化为一个LIS问题

首先设置一个数组 $id[]$ 用来存入a数组里面的每个出现的数的下标

然后将b数组转化为b'数组，即 $b'[i] = id[b[i]]$ 用来表示：b数组中当前数在a数组中对应的下标

那么要想b中的某个序列在a中也是其中的序列

就需要我们得到的这个b'中的某个子序列，在a中出现过就行了，同时要保证在a中的下标是顺序的
所以问题可以转化为求b'数组的最长上升子序列

const int N = 1e6 + 10;

int id[N], n;
vector<int> vec;

int main(){
    read(n);
    for(int i = 1, x; i <= n; i ++)  read(x), id[x] = i;
    for(int i = 1, x; i <= n; i ++){ read(x);
        if(!id[x]) continue;//注意：如果没出现过那就不要加进去了
        if(vec.empty() || vec.back() < id[x]) vec.push_back(id[x]);
        else                                  vec[lower_bound(vec.begin(), vec.end(), id[x]) - vec.begin()] = id[x];
    }write(vec.size());
    return 0;
}

数塔问题

重在决策处理与遍历顺序
因为我们要收集最高点的最大值
只能通过下面的子节点给予贡献
所以从下向上，层层决策累加求得
$dp[x][y] += max(dp[x + 1][y], dp[x + 1][y + 1])$ 选取左右节点最大值

const int N = 110;
int dp[N][N];
int n;

int main(){
        int cass;
        for ( cass = inputInt(); cass; cass -- ) {
                n = inputInt();
                for ( int i = 1; i <= n; i ++ )
                        for ( int j = 1; j <= i; j ++ )
                                dp[i][j] = inputInt();
                for ( int i = n - 1; i >= 1; i -- )
                        for ( int j = 1; j <= i; j ++ )
                                dp[i][j] += MAX(dp[i + 1][j], dp[i + 1][j + 1]);
                outInt(dp[1][1]); puts("");
        }
        return 0;
}

灵活运用题

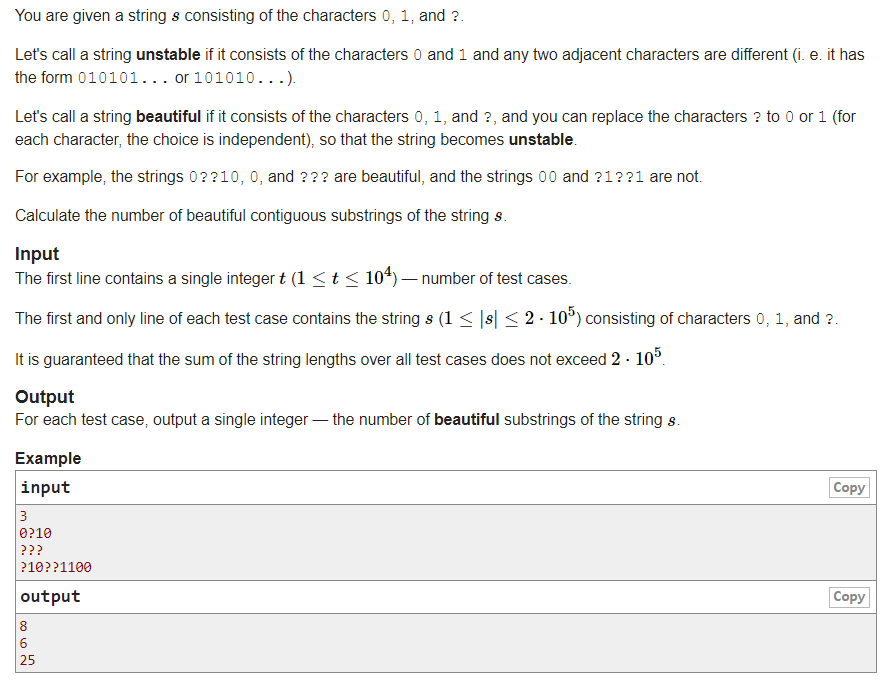
因为'?'可以取0或1
所以这可以被看作一个决策问题
决策就可以联想到dp

在010101...后面如果是一个0
以0结尾的可选子串数量 = 上一步以1结尾的话可选字符串数量+1
此时以1结尾的字符串可选数量，就是0
后面是1同理
如果后面是'?'的话
那么这一位可以放0也可也放1
放0的话以0结尾的可选子串数量 = 上一步以1结尾的话可选字符串数量+1
放1的话以1结尾的可选子串数量 = 上一步以0结尾的话可选字符串数量+1

这样dp推导公式就有了
dp1表示这一位以1结尾的串构成的成立子串值
dp0表示这一位以0结尾的串构成的成立子串值

$$\begin{cases} & \text{if(s[i] = '0')}\qquad dp0[i] = dp1[i - 1] + 1, dp1[i] = 0; \\ & \text{if(s[i] == '1')}\quad\;dp1[i] = dp0[i - 1] + 1, dp0[i] = 0;\\ & \text{if(s[i] == '?')}\quad\;dp1[i] = dp0[i - 1] + 1, dp0[i] = dp1[i - 1] + 1; \end{cases}$$

由于同一段[l, r]不能选两次
所以每次取MAX累加就行了

inline void solve(){
        string s; cin >> s;
        int n = s.size();
        ll res = 0;
        ll dp1[n + 10] = {0};
        ll dp0[n + 10] = {0};

        if(s[0] == '0')      dp0[0] = 1;
        else if(s[0] == '1') dp1[0] = 1;
        else if(s[0] == '?') dp1[0] = dp0[0] = 1;

        for(int i = 1; i < n; i ++){
                if(s[i] == '0')      dp0[i] = dp1[i - 1] + 1, dp1[i] = 0;
                else if(s[i] == '1') dp1[i] = dp0[i - 1] + 1, dp0[i] = 0;
                else                 dp1[i] = dp0[i - 1] + 1, dp0[i] = dp1[i - 1] + 1;
        }
        for(int i = 0; i < n; i ++)  res += MAX(dp1[i],  dp0[i]);
        cout << res << endl;
}

int main(){
        int cass;
        for ( cass = inputInt(); cass; cass -- ) {
                solve();
        }
        _REGAL;
}